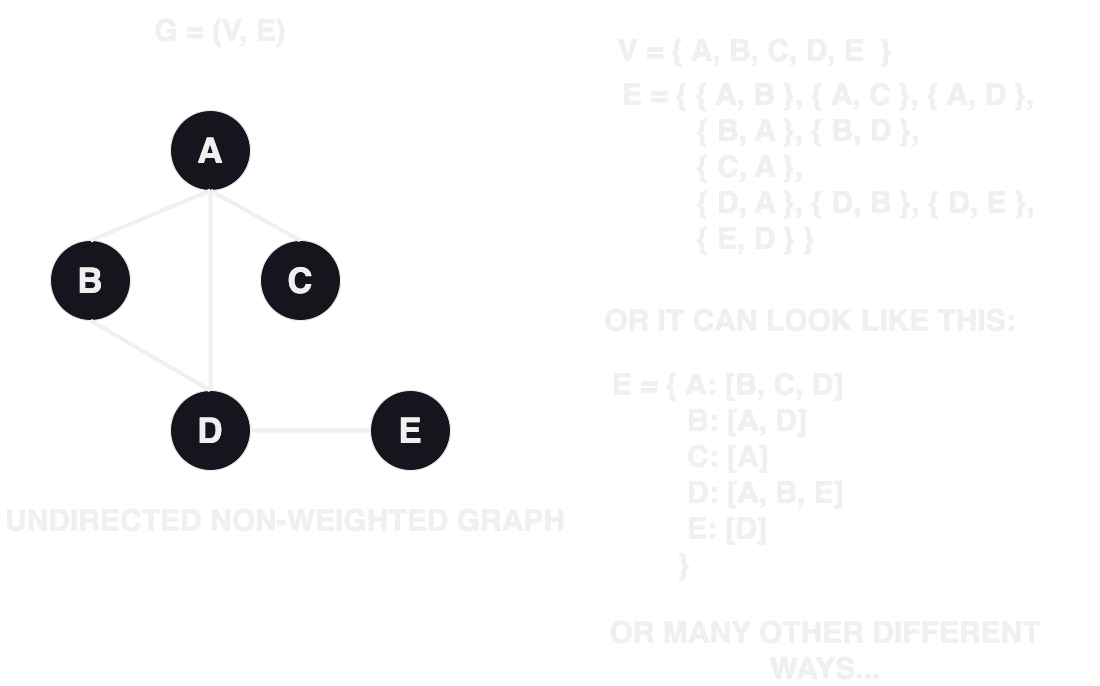
Graph
A graph is a way to represent a set of vertices (also known as nodes) and the connections between them,
called edges. It is a fundamental data structure used to model relationships between objects.
In a graph, vertices can represent any kind of entities, such as cities in a map, web pages in a
website, or even individuals in a social network. The edges represent the relationships or connections
between these entities.
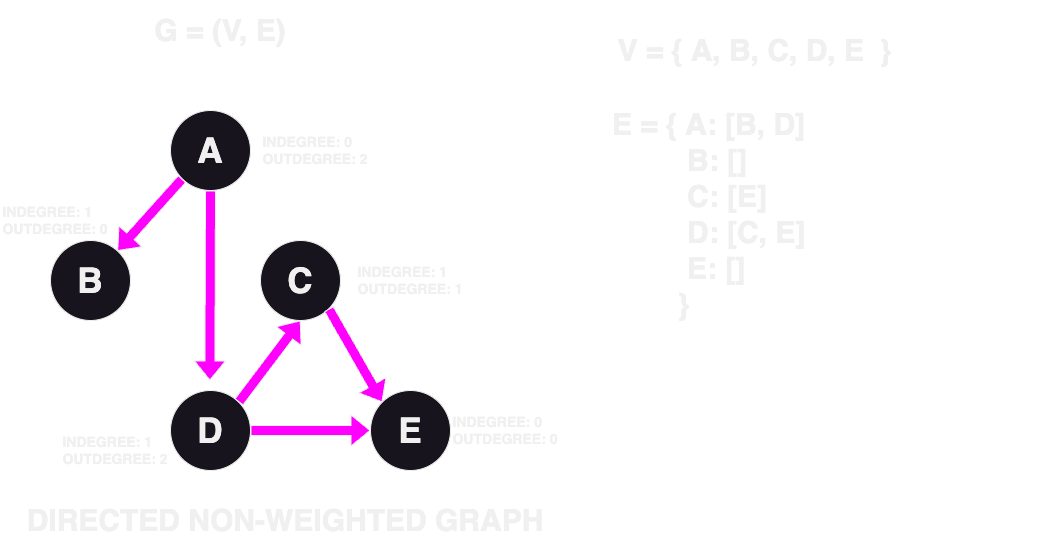
Directed graph
A directed graph, also known as a digraph, is a type of graph where each edge is assigned a direction.
This means that the edge connects a source vertex to a target vertex, indicating a one-way relationship
between them.
Directed graphs are commonly used to represent relationships or flows between entities in various
fields, such as computer networks, social networks, logistical systems, and more. For example, in a
transportation system, directed edges could represent the flow of vehicles from one intersection to
another, while in a social network, directed edges could represent the direction of a friendship, or
following relationship.
In a directed graph, we classify the vertices into two categories based on their connectivity with the
edges - "in-degree" and "out-degree". The in-degree of a vertex represents how many edges point towards
it, while the out-degree represents how many edges start from it.
Undirected graph
Undirected graphs are a common data structure used in computer science to represent a collection of nodes
and the connections between them. In this type of graph, the connections between nodes are
bidirectional, meaning that if node A is connected to node B, then node B is also connected to node A.
For example, consider a social network where each person is represented by a node, and the connections
between nodes indicate friendships. In an undirected graph, if Person A is friends with Person B, then
Person B is also friends with Person A.
Undirected graphs have various algorithms associated with them, including:
Depth-First Search (DFS): DFS can be used to find a path between two nodes, check
connectivity, or detect cycles in a graph.
Breadth-First Search (BFS): BFS is useful for finding the shortest path between two
nodes or discovering if a graph is bipartite.
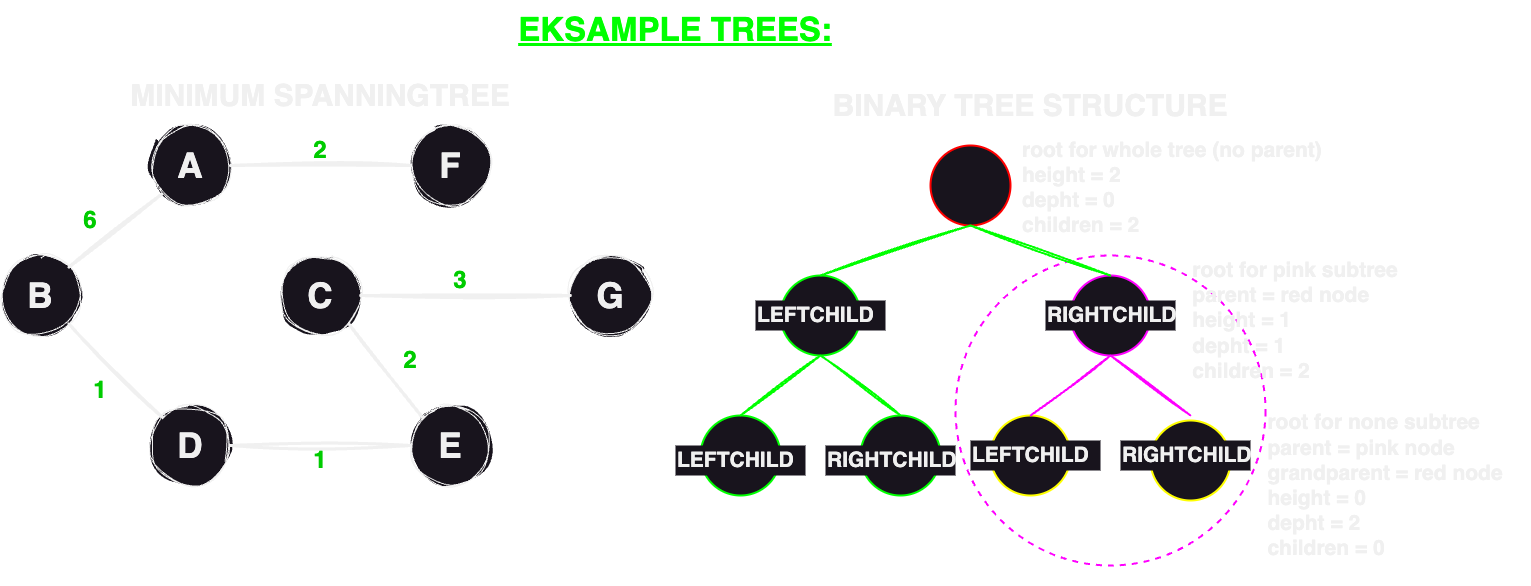
Minimum Spanning Tree (MST): An MST is a subgraph that connects all the nodes with the
minimum total edge weight, without creating any cycles.

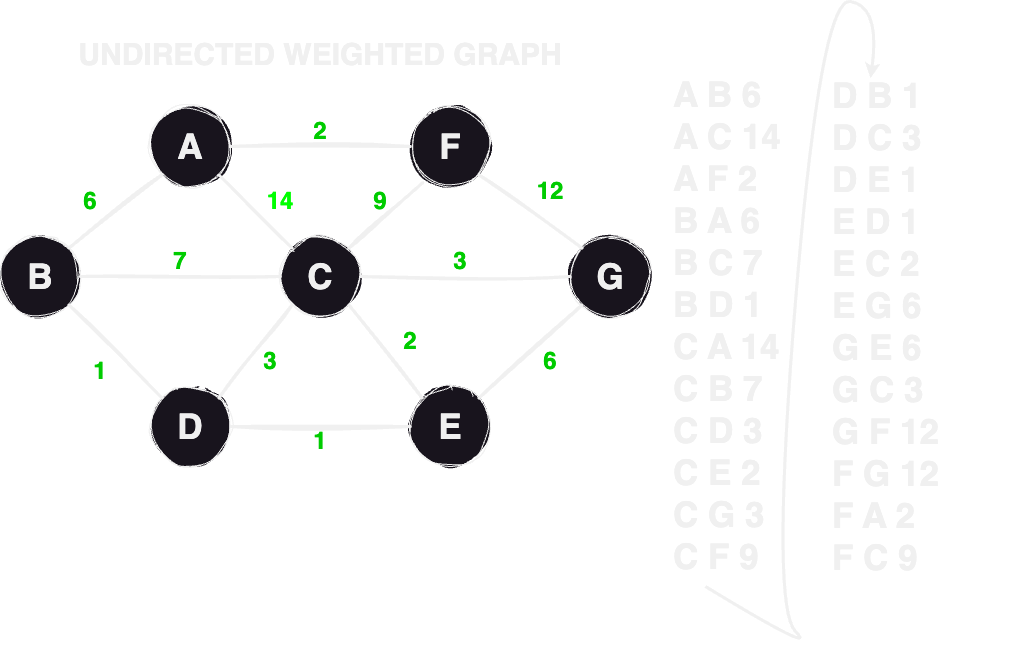
Weighted graph
A weighted graph is a type of graph in which each edge is assigned a numerical value called a weight.
These weights represent the "cost" or "distance" associated with traversing that edge. The main purpose
of using weights in a graph is to model real-world scenarios more accurately, where different edges may
have varying costs or importance.
In a weighted graph, paths between vertices are not just determined by the presence or absence of edges,
but also by the cumulative weight of those edges. This allows for more precise analysis and
decision-making, as it considers the actual cost of moving from one vertex to another.
The weights assigned to edges can represent various factors, such as distance, time, cost, or any other
relevant metric, depending on the context of the problem being modeled. Weighted graphs find numerous
applications in fields like transportation planning, network routing, optimization problems, and many
others.
Tree
All trees are graphs, but not all graphs are trees. Trees is essentially undirected graphs that is
connected and acyclic, meaning that there are no cycles or loops in the graph. Because of that we know
that all trees have |V|-1 edges, one less than the amount of vertices in the graph(tree).
In a tree, each pair of vertices is connected by exactly one unique path. This means that there is only
one way to travel between any two vertices in the graph. Additionally, there are no closed loops or
circuits in a tree, ensuring that there are no repeated edges or vertices.
A tree has a hierarchical structure with a designated root vertex, from which all other vertices are
connected through edges. Each vertex in the tree, except for the root, has exactly one parent vertex and
zero or more child vertices. This parent-child relationship forms a branching structure, similar to the
branches of a tree, which is why it is called a tree.
Tree structures:
Binary trees Vertices have no more than 2 children
Binary search-tree: Vertices have no more than 2 children. Parents are larger than every
node in its left subtree and smaller than (equal) all nodes in its right subtree.
Minimum Spanning Tree (MST): An MST is a subgraph that connects all the nodes with the
minimum total edge weight, without creating any cycles. If you instead connect all the nodes with the
maximum total edge weight you will get a maximum spanning tree.
AVL-Trees: Stable binary-search tree. That means all AVL trees are binary search trees,
but not all binary search tress are AVL trees. Keeps control over the height of each node, if two
subtrees have a height difference < -1 or> 1 it will perform rotation(s) to stabilize the tree. This
ensures a nice tree structure that has the minimal overall height it can have. This supports quick
traversing.
Red/black trees The root is 'colored' black, the rest can be colored either red or
black. Red nodes cant have red children. There has to be equally amont of black nodes in every path
from the root to the leafnodes. This gives a stable tree structure, almost as stable as AVl and it
requires less rotations.